Problem
“It is the question which is to be solved. For solving the problem it needs to be precisely defined. The definition means, defining the start state, goal state, other valid states and transitions”.
State space search
“It is complete set of states including start and goal states, where the answer of the problem is to be searched”.
A state space representation allows for the formal definition of a problem which makes the movement from initial state to the goal state quite easily. So we can say that various problems like planning, learning, theorem proving etc. are all essentially search problems only.
For Example:
The eight tile puzzle problem formulation
The eight tile puzzle consist of a 3 by 3 (3*3) square frame board which holds 8 movable tiles numbered 1 to 8. One square is empty, allowing the adjacent tiles to be shifted. The objective of the puzzle is to find a sequence of tile movements that leads from a starting configuration to a goal configuration.
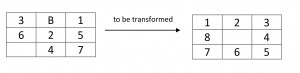
The states of 8 tile puzzle are the different permutations of the tiles within frame.
Lets do a standard formulation of this problem now.
States: It specifies the location of each of the 8 tiles and the blank in one of the nine squares.
Initial state : Any state can be designated as the initial state.
Goal : Many goal configurations are possible one such is shown in the figure
Legal moves ( or state) : They generate legal states that result from trying the four actions-
- Blank moves left
- Blank moves right
- Blank moves up
- Blank moves down
Path cost: Each step costs 1, so the path cost is the number of steps in the path.
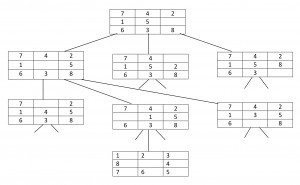
The tree diagram showing the search space is shown in figure.