Hill climbing is an example of an informed search method because it uses information about the search space to search in a reasonably efficient manner. The Hill climbing search always moves towards the goal. Using heuristics it finds which direction will take it closest to the goal. The name hill climbing is derived from simulating the situation of a person climbing the hill. A hiker is lost halfway up/down a mountain at night. His camp is at the top of the mountain. Even though it is dark, the hiker the hiker knows that every step he takes up the mountain is a step towards his goal.
The algorithm for Hill climbing is as follows:
- Evaluate the initial state, if it is goal state quit otherwise make current state as initial state.
- Select a new operator that could be applied to this state and generate a new state.
- Evaluate the new state
- If this new state is closer to the goal state, than current state make the new state as the current state.
- If it is not better ignore this state and proceed with current state.
- If the current state is goal state or no new operators are available, quit. Otherwise repeat from 2.
Problems with Hill climbing
There are three problems encountered in hill climbing technique:
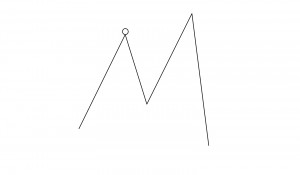
- Local maxima
It is a state which is better than all of its neighbours but is not better than some other states which are farther away. It is a state where we have climbed to the top of the hill, and missed the mountain.
Solution to the problem
i. One possible solution is backtracking.
We can backtrack to some earlier node and try to go in a different direction to attain the global peak. We can maintain a list of paths almost taken and go back to one of them if the path that was taken leads to a dead end.
ii. Another solution can be a list of promising plan.
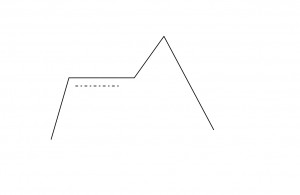
- Plateau
It is a state where everything around is about as good as where we are currently. In other words a flat area of the search space in which all neighbouring states have the same value.
Solution to the problem
i. A big jump in some direction can be done in order to get to a new section of search space. This method is recommended as in a plateau all neighbouring points have the same value.
ii. Another solution is to apply small steps several times in the same direction. This depends on the rules available.
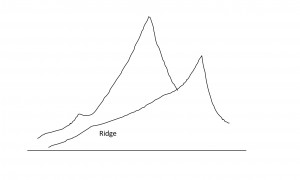
- Ridges
It is a special kind of local maximum. It is an area of the search space which is higher than the surrounding areas and that itself has a slope. We cannot travel the ridge by single moves as the orientation of the high region compared to the set of available moves makes it impossible.
Solution to the problem
i. Trying different paths at the same time is a solution. We can apply two or more rules before doing the test. This corresponds to moving in several directions at once.
ii. Bidirectional search can be useful here.
Advantages of Hill Climbing
- It can be used in conversions as well as discrete domains
Disadvantages of Hill Climbing
- It is not an efficient method.
- It is not suited to problems where the value of the heuristic function drops off suddenly when the solution may be in sight.
- It is a local method as it looks at the immediate solution and decides about the next step to be taken rather than exploring all consequences before taking a move.